György Tegze¹, László Gránásy^1,2, Gyula Tóth³, Jack F. Douglas⁴, Tamás Pusztai¹

¹Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
²BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
³Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
⁴Polymers Division, National Institute of Standards and Technology,Gaithersburg, MD, 20899, USA

The present work explores the ubiquitous morphological changes in crystallizing systems with increasing thermodynamic driving force based on a novel dynamic density functional theory. A colloidal 'soft' material is chosen as a model system for our investigation since there are careful colloidal crystallization observations at a particle scale resolution for comparison, which allows for a direct verification of our simulation predictions. We particularly focus on a theoretically unanticipated, and generic, morphological transition leading to progressively irregular-shaped single crystals in both colloidal and polymeric materials with an increasing thermodynamic driving force. Our simulation method significantly extends previous 'phase field' simulations by incorporating a minimal description of the 'atomic' structure of the material, while allowing simultaneously for a description of large scale crystal growth. We discover a 'fast' mode of crystal growth at high driving force, suggested before in experimental colloidal crystallization studies, and find that the coupling of this crystal mode to the well-understood 'diffusive' or 'slow' crystal growth mode (giving rise to symmetric crystal growth mode and dendritic crystallization as in snowflakes by the Mullins-Sekerka instability) can greatly affect the crystal morphology at high thermodynamic driving force. In particular, an understanding of this interplay between these fast and slow crystal growth modes allows us to describe basic crystallization morphologies seen in both colloidal suspensions with increasing particle concentration and crystallizing polymer films with decreasing temperature: compact symmetric crystals, dendritic crystals, fractal-like structures, and then a return to compact symmetric single crystal growth again.

Gyula Tóth¹, György Tegze², Tamás Pusztai², Gergely Tóth³, László Gránásy^2,4

¹Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
²Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
³Institute of Chemistry, Eötvös University, P.O. Box 32, H-1518 Budapest, Hungary
⁴BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom

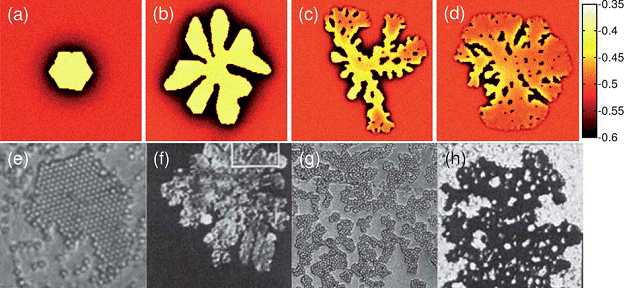
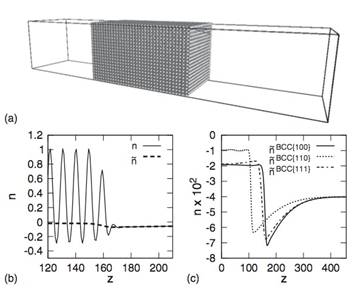
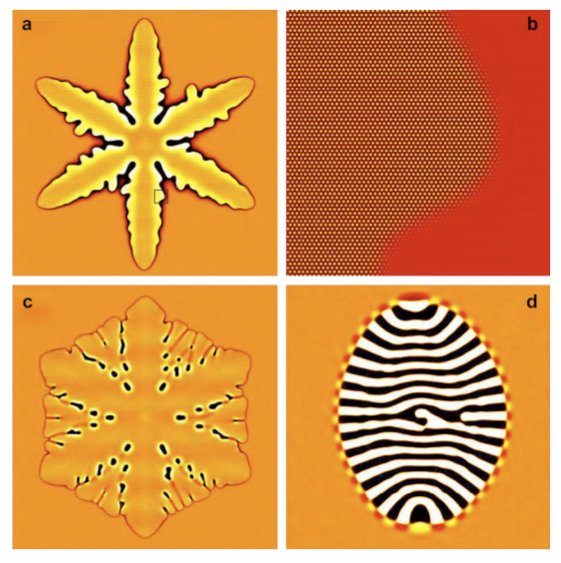
We apply a simple dynamical density functional theory, the phase-field crystal (PFC) model of overdamped conservative dynamics, to address polymorphism, crystal nucleation, and crystal growth in the diffusion-controlled limit. We refine the phase diagram for 3D, and determine the line free energy in 2D and the height of the nucleation barrier in 2D and 3D for homogeneous and heterogeneous nucleation by solving the respective Euler-Lagrange (EL) equations. We demonstrate that, in the PFC model, the body-centered cubic (bcc), the face-centered cubic (fcc), and the hexagonal close-packed structures (hcp) compete, while the simple cubic structure is unstable, and that phase preference can be tuned by changing the model parameters: close to the critical point the bcc structure is stable, while far from the critical point the fcc prevails, with an hcp stability domain in between. We note that with increasing distance from the critical point the equilibrium shapes vary from the sphere to specific faceted shapes: rhombic dodecahedron (bcc), truncated octahedron (fcc), and hexagonal prism (hcp). Solving the equation of motion of the PFC model supplied with conserved noise, solidification starts with the nucleation of an amorphous precursor phase, into which the stable crystalline phase nucleates. The growth rate is found to be time dependent and anisotropic; this anisotropy depends on the driving force. We show that due to the diffusion-controlled growth mechanism, which is especially relevant for crystal aggregation in colloidal systems, dendritic growth structures evolve in large-scale isothermal single-component PFC simulations. An oscillatory effective pair potential resembling those for model glass formers has been evaluated from structural data of the amorphous phase obtained by instantaneous quenching. Finally, we present results for eutectic solidification in a binary PFC model.

László Gránásy^1,2, György Tegze¹, Gyula Tóth³, Tamás Pusztai¹

¹Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
²BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
³Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.

A simple dynamical density functional theory, the phase-field crystal (PFC) model, was used to describe homogeneous and heterogeneous crystal nucleation in two-dimensional (2D) monodisperse colloidal systems and crystal nucleation in highly compressed Fe liquid. External periodic potentials were used to approximate inert crystalline substrates in addressing heterogeneous nucleation. In agreement with experiments in 2D colloids, the PFC model predicts that in 2D supersaturated liquids, crystalline freezing starts with homogeneous crystal nucleation without the occurrence of the hexatic phase. At extreme supersaturations, crystal nucleation happens after the appearance of an amorphous precursor both in two and three dimensions. Contrary to expectations based on the classical nucleation theory, it is shown that corners are not necessarily favourable places for crystal nucleation. Finally, it is shown that by adding external potential terms to the free energy, the PFC theory can be used to model colloid patterning experiments.

György Tegze¹, László Gránásy^1,2, Gyula Tóth³, Frigyes Podmaniczky¹, A Jaatinen⁴, T Ala-Nissila⁴, Tamás Pusztai¹

¹Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
²BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
³Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
⁴Department of Applied Physics, Helsinki University of Technology, Post Office Box 1100, FI-02015 TKK, Finland

We use a simple density functional approach on a diffusional time scale, to address freezing to the body-centered cubic (bcc), hexagonal close-packed (hcp), and face-centered cubic (fcc) structures. We observe faceted equilibrium shapes and diffusion-controlled layerwise crystal growth consistent with two- dimensional nucleation. The predicted growth anisotropies are discussed in relation with results from experiment and atomistic simulations. We also demonstrate that varying the lattice constant of a simple cubic substrate, one can tune the epitaxially growing body-centered tetragonal structure between bcc and fcc, and observe a Mullins-Sekerka/Asaro-Tiller-Grinfeld-type instability.

György Tegze¹, Gurvinder Bansel², Gyula Tóth³, Tamás Pusztai¹, Zhongyun Fan², László Gránásy^1,2

¹Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
²BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
³Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.

We present an efficient method to solve numerically the equations of dissipative dynamics of the binary phase-field crystal model proposed by Elder et al. [K.R. Elder, M. Katakowski, M. Haataja, M. Grant, Phys. Rev. B 75, 064107 (2007)] characterized by variable coefficients. Using the operator splitting method, the problem has been decomposed into sub-problems that can be solved more efficiently. A combination of non-trivial splitting with spectral semi-implicit solution leads to sets of algebraic equations of diagonal matrix form. Extensive testing of the method has been carried out to find the optimum balance among errors associated with time integration, spatial discretization, and splitting. We show that our method speeds up the computations by orders of magnitude relative to the conventional explicit finite difference scheme, while the costs of the pointwise implicit solution per timestep remains low. Also we show that due to its numerical dissipation, finite differencing can not compete with spectral differencing in terms of accuracy. In addition, we demonstrate that our method can efficiently be parallelized for distributed memory systems, where an excellent scalability with the number of CPUs is observed.