Gyula Tóth¹, Tamás Pusztai², László Gránásy^2,3

¹Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
²Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
³BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom

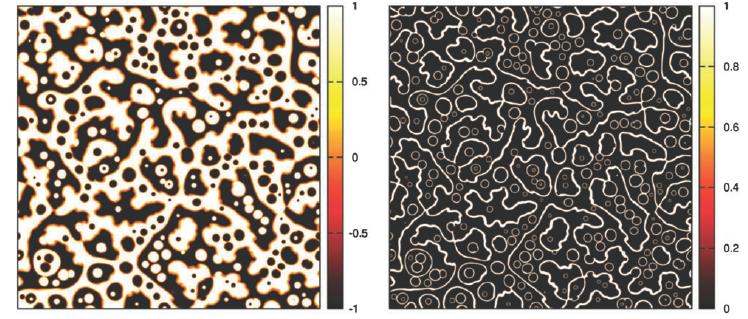
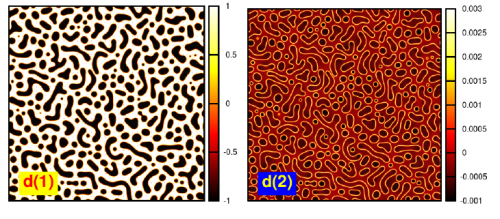
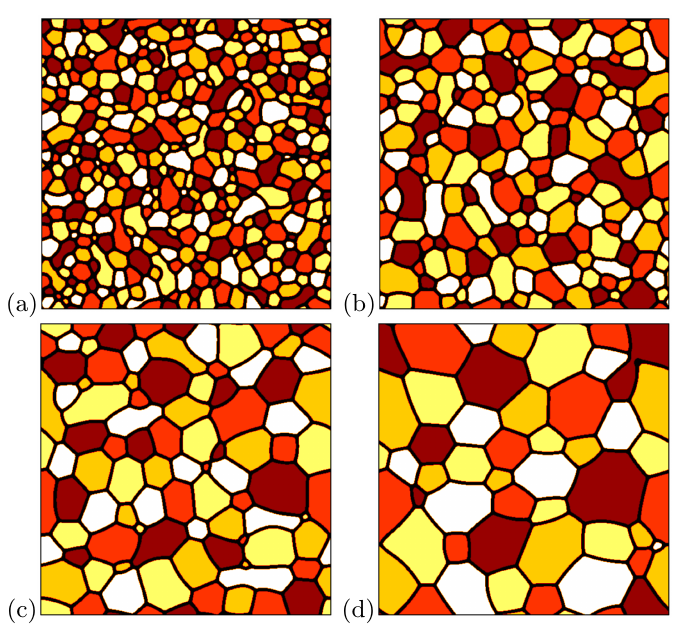
We present a new multiphase-field theory for describing pattern formation in multi-domain and/or multi-component systems. The construction of the free energy functional and the dynamic equations is based on criteria that ensure mathematical and physical consistency. We first analyze previous multiphase-field theories, and identify their advantageous and disadvantageous features. On the basis of this analysis, we introduce a new way of constructing the free energy surface, and derive a generalized multiphase description for arbitrary number of phases (or domains). The presented approach retains the variational formalism; reduces (or extends) naturally to lower (or higher) number of fields on the level of both the free energy functional and the dynamic equations; enables the use of arbitrary pairwise equilibrium interfacial properties; penalizes multiple junctions increasingly with the number of phases; ensures non-negative entropy production, and the convergence of the dynamic solutions to the equilibrium solutions; and avoids the appearance of spurious phases on binary interfaces. The new approach is tested for multi-component phase separation and grain coarsening.

Gyula Tóth¹, Mojdeh Zarifi, Bjørn Kvamme²

¹Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
²Institute of Physics and Technology, University of Bergen, Allégaten 55, N-5007 Bergen, Norway

In this paper, a generalization of the Cahn-Hilliard theory of binary liquids is presented for multicomponent incompressible liquid mixtures. First, a thermodynamically consistent convection-diffusion-type dynamics is derived on the basis of the Lagrange multiplier formalism. Next, a generalization of the binary Cahn-Hilliard free-energy functional is presented for an arbitrary number of components, offering the utilization of independent pairwise equilibrium interfacial properties. We show that the equilibrium two-component interfaces minimize the functional, and we demonstrate that the energy penalization for multicomponent states increases strictly monotonously as a function of the number of components being present. We validate the model via equilibrium contact angle calculations in ternary and quaternary (four-component) systems. Simulations addressing liquid-flow-assisted spinodal decomposition in these systems are also presented.

Gyula Tóth¹, Bjørn Kvamme²

¹Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
²Institute of Physics and Technology, University of Bergen, Allégaten 55, N-5007 Bergen, Norway

In this paper the quantitative applicability of van der Sman/van der Graaf type Ginzburg–Landau theories of surfactant assisted phase separation [van der Sman et al., Rheol. Acta, 2006, 46, 3] is studied for real systems displaying high surfactant concentrations at the liquid–liquid interface. The model is applied for the water/heptane/asphaltene system (a model of heavy crude oil), for which recent molecular dynamics (MD) simulations provide microscopic data needed to calibrate the theory. A list of general requirements is set up first, which is then followed by analytical calculations of the equilibrium properties of the system, such as the equilibrium liquid densities, the adsorption isotherm and the interfacial tension. Based on the results of these calculations, the model parameters are then determined numerically, yielding a reasonable reproduction of the MD density profiles. The results of time-dependent simulations addressing the dynamical behaviour of the system will also be presented. It will be shown that the competition between the diffusion and hydrodynamic time scales can lead to the formation of an emulsion. We also address the main difficulties and limitations of the theory regarding quantitative modelling of surfactant assisted liquid phase separation.

Gyula Tóth¹, Bjørn Kvamme²

¹Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
²Institute of Physics and Technology, University of Bergen, Allégaten 55, N-5007 Bergen, Norway

In this paper diffuse interface models of surfactant-assisted liquid-liquid phase separation are addressed. We start from the generalized version of the Ginzburg-Landau free-energy-functional-based model of van der Sman and van der Graaf. First, we analyze the model in the constant surfactant approximation and show the presence of a critical point at which the interfacial tension vanishes. Then we determine the adsorption isotherms and investigate the validity range of previous results. As a key point of the work, we propose a new model of the van der Sman/van der Graaf type designed for avoiding both unwanted unphysical effects and numerical difficulties present in previous models. In order to make the model suitable for describing real systems, we determine the interfacial tension analytically more precisely and analyze it over the entire accessible surfactant load range. Emerging formulas are then validated by calculating the interfacial tension from the numerical solution of the Euler-Lagrange equations. Time-dependent simulations are also performed to illustrate the slowdown of the phase separation near the critical point and to prove that the dynamics of the phase separation is driven by the interfacial tension.