R. Zanella, G. Tegze, R. Le Tellier, H. Henry
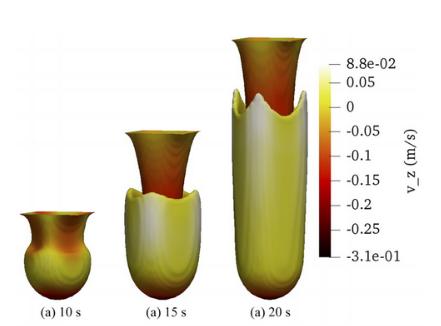
We report on two- and three-dimensional numerical simulations of Rayleigh–Taylor instabilities in immiscible fluids. A diffuse-interface model that combines the Cahn–Hilliard equation, governing the evolution of the volume fraction of one fluid, and the Navier–Stokes equations, governing the bulk velocity and pressure, is used. The study is limited to low Atwood numbers owing to the use of the Boussinesq approximation. The code is based on a pseudo-spectral method. A linear analysis is first performed in a two-dimensional case of Rayleigh–Taylor instability to confirm that the model very well captures this phenomenon in the case of inviscid or viscid fluids. One key aspect of this work is that the influence of the thermodynamic parameters related to the Cahn–Hilliard equation (interface thickness and mobility) is quantitively studied. Three-dimensional results of Rayleigh–Taylor instabilities in viscous fluids are then presented to show the possibilities of this modeling. We observe the effect of the viscosity and the wavelength of an initial single-mode perturbation on the mass transport during the nonlinear regime.
