Tamás Pusztai1, László Rátkai1, Levente Horváth, László Gránásy1,2
1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
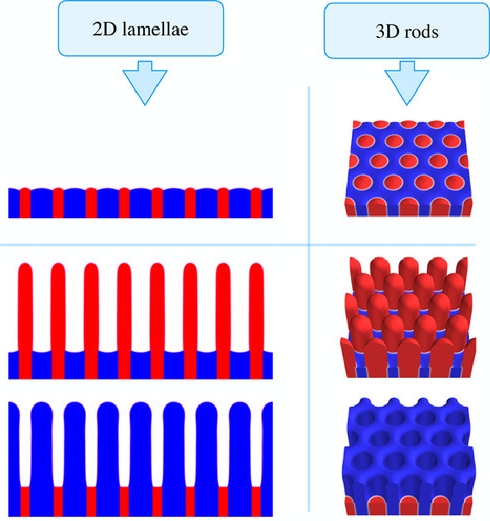
The melting of 2D lamellar and 3D rod eutectic structures was studied by multi-phase-field simulations. A binary model eutectic system was investigated in a standard directional solidification setup. Switching from solidification to melting was realised by inverting the pulling speed of the sample. Steady state melting profiles were obtained as the long-time solutions of the evolution equations solved in the minimal representative domains of the periodic structures. Series of simulations were performed using different volume fractions of the initial solid phases, different values of the temperature gradient, and different widths of the simulation domain. It was found that melting occurs with a nearly flat interface if the average composition of the initial solid structure is equal to the eutectic composition. If the volume fraction of the solid phases is changed and the average composition becomes off-eutectic, then the melting positions of the phases decouple: the phase of sub-eutectic amount will melt near the eutectic temperature, while the phase of super-eutectic amount will melt near its liquidus temperature corresponding to the off-eutectic mean composition. The lamellar/rod spacing imposed by the width of the simulation domain has only minor effect on the interface temperature. Besides the steady states, we could observe two kinds of instabilities in the regime of non-planar melting both in 2D and 3D. By increasing the lamellar spacing, oscillations may appear around the trijunction and along the phase boundaries. By decreasing the lamellar spacing and increasing the pulling speed, the lamellae/rods of the phase that protrude deeper in the melt become thinner and may eventually break up to a series of small spherical particles before melting completely.


