Latest publications

Polycrystalline patterns in far-from-equilibrium freezing: a phase field study

László Gránásy1,2, Tamás Pusztai1, T Börzsönyi, Gyula Tóth3, György Tegze1, James A. Warren4, Jack F. Douglas5

1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
3Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
4Metallurgy Division, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA
5Polymers Division, National Institute of Standards and Technology,Gaithersburg, MD, 20899, USA

We discuss the formation of polycrystalline microstructures within the framework of phase field theory. First, the model is tested for crystal nucleation in a hard sphere system. It is shown that, when evaluating the model parameters from molecular dynamics simulations, the phase field theory predicts the nucleation barrier for hard spheres accurately. The formation of spherulites is described by an extension of the model that incorporates branching with a definite orientational mismatch. This effect is induced by a metastable minimum in the orientational free energy. Spherulites are an extreme example of polycrystalline growth, a phenomenon that results from the quenching of orientational defects (grain boundaries) into the solid as the ratio of the rotational to the translational diffusion coefficient is reduced, as is found at high undercoolings. It is demonstrated that a broad variety of spherulitic patterns can be recovered by changing only a few model parameters.

Topics: Polycrystalline solidification

Philosophical Magazine 86, 3757-3778, (2006)
Download preprint View at Publisher

Phase field theory of liquid phase separation and solidification with melt flow

György Tegze1, László Gránásy1,2

1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom

A phase-field theory of binary liquid phase separation and solidification coupled to fluid flow is presented. The respective equations of motion and Navier-Stokes equations are solved numerically. We incorporate composition and temperature dependent capillary forces. The free energies of the bulk liquid phases are taken from the regular solution model. In the simulations, we observe Marangoni motion of the droplets, and direct and indirect hydrodynamic interactions between the droplets. We observe that capillary effects dramatically accelerate droplet coagulation and that solidification interacts with liquid phase separation.

Proceedings of Modeling of Casting, Welding and Advanced Solidification Processes - Xi 513-520, (2006)
Download preprint View at Publisher

Phase field theory of polycrystalline freezing in three dimensions

Tamás Pusztai1, G Bortel, László Gránásy1,2

1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom

A phase field theory, we proposed recently to describe nucleation and growth in three dimensions (3D), has been used to study the formation of polycrystalline patterns in the alloy systems Al-Ti and Cu-Ni. In our model, the free energy of grain boundaries is assumed proportional to the angular difference between the adjacent crystals expressed in terms of the differences of the four symmetric Euler parameters called quaternions. The equations of motion for these fields have been obtained from variational principles. In the simulations cubic crystal symmetries are considered. We investigate the evolution of polydendritic morphology, present simulated analogies of the metallographic images, and explore the possibility of modeling solidification in thin layers. Transformation kinetics in the bulk and in thin films is discussed in terms of the Johnson-Mehl-Avrami-Kolmogorov approach.

Proceedings of Modeling of Casting, Welding and Advanced Solidification Processes - Xi 409-416, (2006)
Download preprint

Multi-scale approach to CO2-hydrate formation in aqueous solution: Phase field theory and molecular dynamics. Nucleation and growth

György Tegze1, Tamás Pusztai1, Gyula Tóth2, László Gránásy1,3, A Svandal, T Buanes, T Kuznetsova, Bjørn Kvamme4

1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
3BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
4Institute of Physics and Technology, University of Bergen, Allégaten 55, N-5007 Bergen, Norway

A phase field theory with model parameters evaluated from atomistic simulations/experiments is applied to predict the nucleation and growth rates of solid CO2 hydrate in aqueous solutions under conditions typical to underwater natural gas hydrate reservoirs. It is shown that under practical conditions a homogeneous nucleation of the hydrate phase can be ruled out. The growth rate of CO2 hydrate dendrites has been determined from phase field simulations as a function of composition while using a physical interface thickness 0.85±0.07 nm evaluated from molecular dynamics simulations. The growth rate extrapolated to realistic supersaturations is about three orders of magnitude larger than the respective experimental observation. A possible origin of the discrepancy is discussed. It is suggested that a kinetic barrier reflecting the difficulties in building the complex crystal structure is the most probable source of the deviations.

Journal of Chemical Physics 124, 234710, (2006)
Download preprint View at Publisher

Phase field theory of crystal nucleation and polyerystalline growth: A review

László Gránásy1,2, Tamás Pusztai1, T Börzsönyi, Gyula Tóth3, György Tegze1, James A. Warren4, Jack F. Douglas5

1Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
2BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
3Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
4Metallurgy Division, National Institute of Standards and Technology, Gaithersburg, Maryland 20899, USA
5Polymers Division, National Institute of Standards and Technology,Gaithersburg, MD, 20899, USA

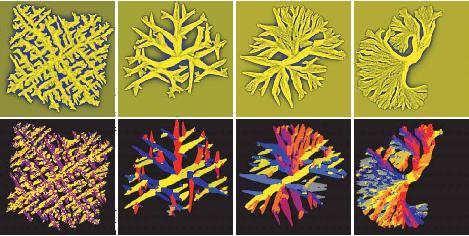
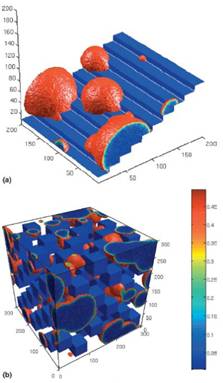
We briefly review Our recent modeling of crystal nucleation and polycrystalline growth using a phase field theory. First, we consider the applicability of phase field theory for describing crystal nucleation in a model hard sphere Fluid. It is shown that the phase field theory accurately predicts the nucleation barrier height for this liquid when the model parameters are fixed by independent Molecular dynamics calculations. We then address various aspects of polycrystalline solidification and associated crystal pattern formation at relatively long timescales. This late stage growth regime, which is not accessible by Molecular dynamics, involves nucleation at the growth front to create new crystal grains in addition to the effects of primary nucleation. Finally, we consider the limit of extreme polycrystalline growth, where the disordering effect due to prolific grain formation leads to isotropic growth patterns at long times, i.e., spherulite formation. Our model of spherulite growth exhibits branching at fixed grain misorientations, induced by the inclusion of a metastable minimum in the orientational free energy. It is demonstrated that a broad variety of spherulitic patterns can be recovered by changing only a few model parameters.

Topics: Polycrystalline solidification

Journal of Materials Research 21, 309-319, (2006)
Download preprint View at Publisher

Pages