Gyula Tóth1, György Tegze2, Tamás Pusztai2, Gergely Tóth3, László Gránásy2,4
1Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
2Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
3Institute of Chemistry, Eötvös University, P.O. Box 32, H-1518 Budapest, Hungary
4BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
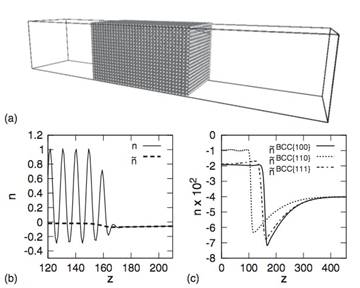
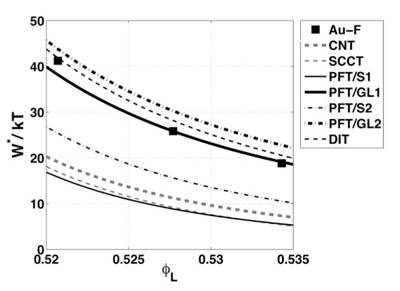
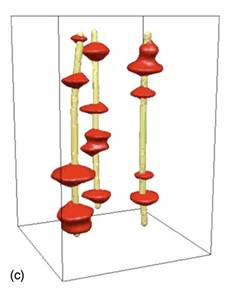
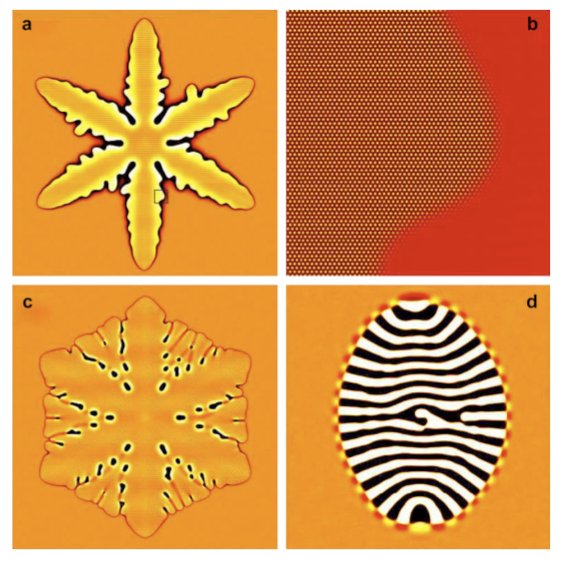
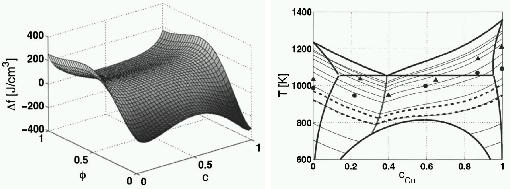
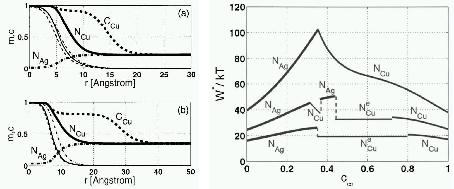
We apply a simple dynamical density functional theory, the phase-field crystal (PFC) model of overdamped conservative dynamics, to address polymorphism, crystal nucleation, and crystal growth in the diffusion-controlled limit. We refine the phase diagram for 3D, and determine the line free energy in 2D and the height of the nucleation barrier in 2D and 3D for homogeneous and heterogeneous nucleation by solving the respective Euler-Lagrange (EL) equations. We demonstrate that, in the PFC model, the body-centered cubic (bcc), the face-centered cubic (fcc), and the hexagonal close-packed structures (hcp) compete, while the simple cubic structure is unstable, and that phase preference can be tuned by changing the model parameters: close to the critical point the bcc structure is stable, while far from the critical point the fcc prevails, with an hcp stability domain in between. We note that with increasing distance from the critical point the equilibrium shapes vary from the sphere to specific faceted shapes: rhombic dodecahedron (bcc), truncated octahedron (fcc), and hexagonal prism (hcp). Solving the equation of motion of the PFC model supplied with conserved noise, solidification starts with the nucleation of an amorphous precursor phase, into which the stable crystalline phase nucleates. The growth rate is found to be time dependent and anisotropic; this anisotropy depends on the driving force. We show that due to the diffusion-controlled growth mechanism, which is especially relevant for crystal aggregation in colloidal systems, dendritic growth structures evolve in large-scale isothermal single-component PFC simulations. An oscillatory effective pair potential resembling those for model glass formers has been evaluated from structural data of the amorphous phase obtained by instantaneous quenching. Finally, we present results for eutectic solidification in a binary PFC model.