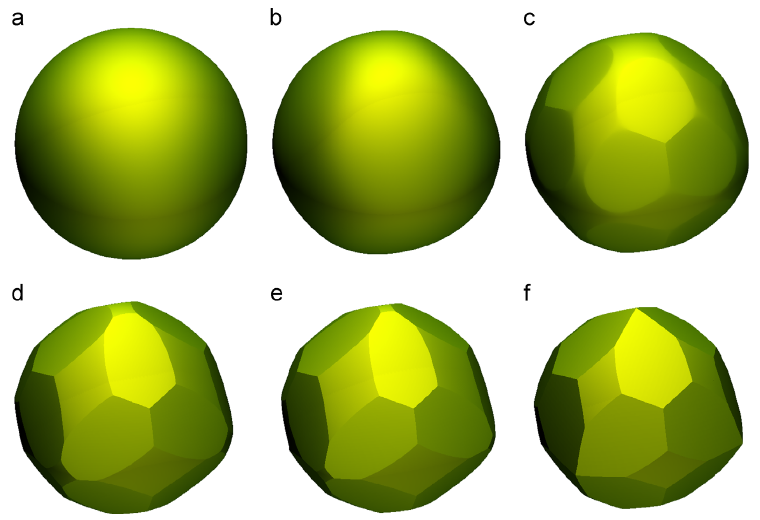
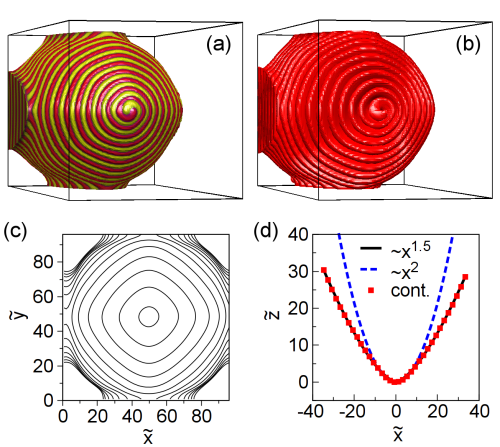
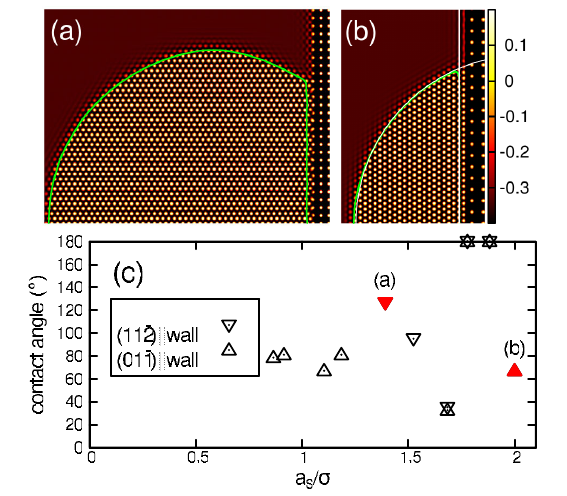
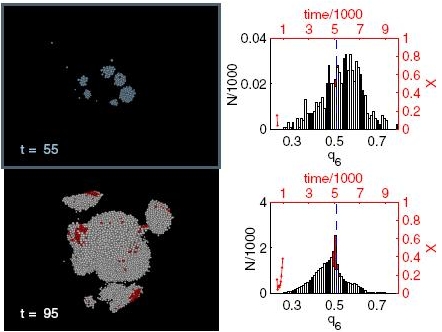
Heike Emmerich1, Hartmut Löwen2, Raphael Wittkowski2, Thomas Gruhn1, Gyula Tóth3, György Tegze4, László Gránásy4,5
1Lehrstuhl für Material- und Prozesssimulation, Universität Bayreuth, D-95440 Bayreuth, Germany
2Institut für Theoretische Physik II, Weiche Materie, Heinrich-Heine-Universität Düsseldorf, D-40225 Düsseldorf, Germany
3Department of Mathematical Sciences, Loughborough University, Loughborough, Leicestershire, LE11 3TU, U.K.
4Institute for Solid State Physics and Optics, Wigner Research Centre for Physics, P.O. Box 49, Budapest H-1525, Hungary
5BCAST, Brunel University, Uxbridge, Middlesex, UB8 3PH, United Kingdom
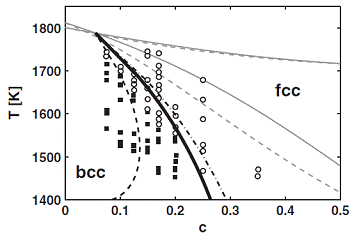
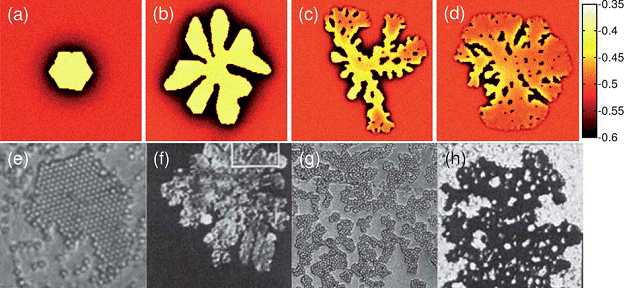
Here, we review the basic concepts and applications of the phase-field-crystal (PFC) method, which is one of the latest simulation methodologies in materials science for problems, where atomic- and microscales are tightly coupled. The PFC method operates on atomic length and diffusive time scales, and thus constitutes a computationally efficient alternative to molecular simulation methods. Its intense development in materials science started fairly recently fol- lowing the work by Elder et al. [Phys. Rev. Lett. 88 (2002), p. 245701]. Since these initial studies, dynamical density functional theory and thermodynamic concepts have been linked to the PFC approach to serve as further theoretical fundamentals for the latter. In this review, we summarize these methodological development steps as well as the most important applications of the PFC method with a special focus on the interaction of development steps taken in hard and soft matter physics, respectively. Doing so, we hope to present today's state of the art in PFC modelling as well as the potential, which might still arise from this method in physics and materials science in the nearby future.